‘Motor neuronal óptico’ puede resolver ecuaciones diferenciales parciales
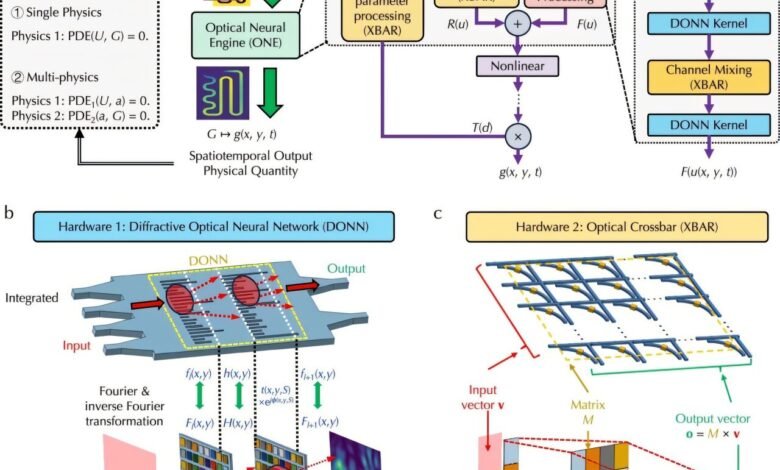
El dispositivo de los investigadores aplica principios de redes neuronales a un marco óptico. Como una onda codificada con un PDE pasa a través de la serie de componentes de uno, sus propiedades cambian y cambian gradualmente, hasta que finalmente representan la solución a la PDE dada. Crédito: Gao Lab, Universidad de Utah
Las ecuaciones diferenciales parciales (PDE) son una clase de problemas matemáticos que representan la interacción de múltiples variables y, por lo tanto, tienen poder predictivo cuando se trata de sistemas físicos complejos. Sin embargo, resolver estas ecuaciones es un desafío perpetuo, y las técnicas computacionales actuales para hacerlo son lentas y costosas.
Ahora, la investigación de la universidad de ingeniería John y Marcia Price de la Universidad de Utah está mostrando una manera de acelerar este proceso: codificar esas ecuaciones a la luz y alimentarlas en su “motor neuronal óptico” recién diseñado o uno.
Uno de los investigadores combina redes neuronales ópticas difractivas y multiplicadores de matriz óptica. En lugar de representar a PDE digitalmente, los investigadores los representaron ópticamente, con variables representadas por las diversas propiedades de una onda de luz, como su intensidad y fase. A medida que una onda pasa a través de la serie de componentes ópticos de uno, esas propiedades cambian y cambian gradualmente, hasta que finalmente representan la solución a la PDE dada.
La investigación fue dirigida por Weilu Gao, profesor asistente en el Departamento de Ingeniería Eléctrica e Informática, y Ruiyang Chen, Ph.D. candidato en el grupo de investigación de GAO. Publicaron un estudio que demuestra este motor neuronal óptico en la revista Nature Communications.
“Las ecuaciones diferenciales parciales son una poderosa herramienta computacional para simular problemas físicos en lugar de realizar experimentos costosos y que requieren mucho tiempo en el mundo real”, dijo Chen. “Sin embargo, el método de simulación numérica actual es lento y requiere muchos recursos informáticos, e incluso las técnicas electrónicas de aprendizaje automático no son lo suficientemente rápidos”.
Las técnicas de aprendizaje automático y las redes neuronales digitales utilizadas actualmente para resolver PDE implican pasar la ecuación a través de una red de nodos computacionales, cada una de las cuales pone su salida a medida que pasa al siguiente nodo. A medida que la señal se abre paso a través de la red, la solución correcta se poneza más y termina como la salida.
El de los investigadores toma este concepto y lo aplica a dispositivos fotónicos.
“El uno toma los datos espacio -temporales de una cantidad física de entrada, que es una función de las posiciones y el tiempo, para predecir los datos espacio -temporales de una cantidad física de salida en función de las posiciones y el tiempo”, dijo Gao.
Las técnicas electrónicas de aprendizaje automático pueden producir una salida similar, pero a velocidades más lentas y mayores costos de energía.
“Este enfoque óptico acelera el proceso de aprendizaje automático y requiere menos energía en comparación con un enfoque electrónico”, dijo el autor principal y ex miembro del laboratorio de GAO, Yingheng Tang, ahora científico de investigación del Laboratorio Nacional de Lawrence Berkeley.
Los investigadores demostraron las capacidades de su uno en una serie de PDE, incluida la ecuación de Darcy Flow, la ecuación magnetostática de Poisson en la desmagnetización y la ecuación de Navier-Stokes en fluido incompresible.
“La ecuación de flujo de Darcy, por ejemplo, describe un flujo de fluido a través de un medio poroso”, dijo Gao. “Dados los datos sobre la permeabilidad y los campos de presión dentro de un medio dado, la arquitectura esencialmente aprende el mapeo entre esas cualidades y puede predecir las propiedades de flujo sin tener que experimentar”.
“Esta investigación ofrece una plataforma versátil y poderosa para el cálculo científico y de ingeniería a gran escala, como la geología y el diseño de chips”, dijo Gao.
Más información: Yingheng Tang et al, motor neuronal óptico para resolver ecuaciones diferenciales parciales científicas, comunicaciones de la naturaleza (2025). Doi: 10.1038/s41467-025-59847-3
Proporcionado por la Universidad de Utah
Cita: ‘Motor neuronal óptico’ puede resolver ecuaciones diferenciales parciales (2025, 10 de junio) Recuperado el 10 de junio de 2025 de https://techxplore.com/news/2025-06-optical-neural-parartial-diferencial-equations.html
Este documento está sujeto a derechos de autor. Además de cualquier trato justo con el propósito de estudio o investigación privada, no se puede reproducir ninguna parte sin el permiso por escrito. El contenido se proporciona solo para fines de información.











